时间地点：

主办单位：讯技光电科技（上海）有限公司；上海讯稷光电科技有限公司；常熟黉论教育咨询有限公司
授课时间：1月22日（一）-23日（二） AM 9:00-16:00
授课地点：上海
课程讲师：讯技光电高级工程师
课程费用：3000 RMB（老师：1000RMB；学生：600RMB）（包含课程材料费、开票税金、午餐费用）

VirtualLab Fusion是一款基于物理光学进行各类光学系统仿真以及衍射和微纳光学元件设计的软件。在光学仿真和设计中，通过求解麦克斯韦方程，能够将波动光学，如干涉，衍射，偏振，相干以及矢量等效应考虑在内以获得系统所有的电磁场信息；同时，应用最新的第二代场追迹技术，极大地提高了计算速度（几乎与光线追迹一样快），从而能够为用户提供准确且高效的仿真技术。 本课程主要面对零基础或少量基础的用户。课程中将会简单介绍软件建模的技术特色以及应用领域和各类文档的使用方法；通过介绍各类光源、光学元件和探测器以及两种模拟引擎——光线追迹和场追迹，来一步步的帮助用户完成各类光学系统的构建以及针对不同的系统进行特性分析；同时，课程中还将通过具体的案例来介绍软件的参数扫描（公差分析）以及参数优化（局部和全局优化）两种优化方法；最后，我们会学习会话编辑器以及堆栈等概念，以学会如何实现衍射和微纳光学器件的基本设计、分析以及优化。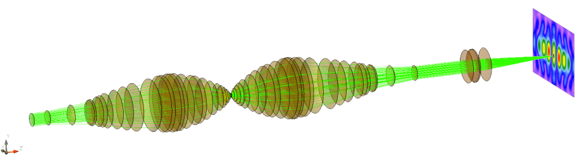

课程将介绍VirtualLab Fusion建模方法以及各类系统过的搭建和分析过程，并进行衍射和微纳元件的设计和分析

主题 第1天：
1. 介绍光学系统中用场追迹和光线追迹仿真光的概念：光线追迹、第二代场追迹和经典场追迹之间的区别。VirtualLab中电磁光建模以及数值数据存储，光场分布可视化，使用不同的物理模型，应用场追迹的概念模拟光在自由空间以及元件间的传输，利用探测器评价光场分布，物理和数值建模误差。
2. VirtualLab文件介绍：光路图，参数运行文件，优化文件，会话编辑器，VirtualLab管理器和属性浏览器。
3. 光学传输系统仿真：准直和聚焦激光传输系统构建，光束波相差，光束参数计算，光线追迹和场追迹，参数运行以及参数优化的使用。
4. 干涉测量系统的仿真：经典白光迈克尔逊干涉系统仿真，相干及部分相干光源建模，干涉图计算。
5. 激光扫描系统的仿真：构建激光扫描系统，并使用参数运行和参数耦合功能，分别使用光线追迹和光场追迹方法来实现激光扫描过程并分析扫描光束特性。
主题 第2天：
1. 衍射和微纳光学元件设计介绍：IFTA介绍，FMM介绍，1f/2系统、近轴远场系统以及角谱系统介绍，会话编辑器应用介绍。
2. 光束整形器设计：折射光束整形器设计，衍射光束整形器设计，圆形或矩形高帽高斯光束整形器设计。
3. 光束扩散器设计：规则扩散器设计，任意扩散器设计，分束器设计。
4. 分束器严格的分析和优化：应用FMM对分束器元件进行严格的分析和优化。
5. 结构导出：相位图转换，结构设计，GDSII文件。

基于课程期间最新版本的VirtualLab Fusion。依据公司动态，可能会对所列主题及其相应时间安排做出调整。可通过 注册并参加此次课程。